why
位置信息在软件以及显示生活中有了越来越多的应用,比如微信里面附近的人,很多游戏里面也加入了地理位置的玩法,让玩家与玩家有更多的互动,提高黏性。
假想这样一个需求:玩家获取附近的人,一起开黑或者某些社交软件获取附近的人交友或者交流,需要怎么实现,假定该软件的使用者比较多。
本身学过一些硬件、传感器的东西,想从计算机硬件和软件的角度写一下自己的理解,首先我们有以下几个问题:
- 我们如何知道自己在世界上的位置
- 如何快速的找到附近的人(附近的旅店)
- 计算机如何处理地球上的位置数据最高效
- geohash及其使用
我们如何知道自己在世界上的位置
面对这个问题的时候,我的第一想法是 手机的GPS模块,手机是一个相对精密的系统,里面当然也包括各种传感器,GPS模块当然也包括,那么我们通过GPS模块就可以拿到我们的位置信息啊,不就是那么简单吗。转念一想,GPS这么小一个东西是怎么知道自己的位置的?
不识庐山真面目,只缘身在此山中。GPS传感器遍布在地球的各个角落,要看到自己的位置,目光肯定要在自己环境之外,要获取在地球的相对位置,需要在地球之外找到合适的角度:
于是,通过地球之外的卫星系统,我们可以通过两个简单的数字来量化自身的位置:(经度,纬度)。
比如可行科学园的位置: (113.942016,22.542644)
附近的人需要的前置基础设施有哪些
我们有了坐标去刻画位置,那么我要找我附近3km的餐馆,需要怎么找?
一个简单的方法如下,根据坐标,计算世界上所有餐馆到我的位置的距离,取其中距离小于3000m的。理论上可以实现,但是方法未免太傻逼了,我找我附近的,还要遍历其他地方的,极其不优雅。
在找到如何实现怎么查找更高效之前,我自己考虑了一下,可以根据GPS 的数据过滤临近的GPS,比如23*开头的附近应该也是 22、24这种,这样找就缩小到一个比较小的区域,但是拿两个制约参数找毕竟不如一个制约参数快,于是又更有效的方式。
geohash:经纬度的一维状态
GeoHash是一种对地理坐标进行编码的方法,它将二维坐标映射为一个字符串。每个字符串代表一个特定的矩形,在该矩形范围内的所有坐标都共用这个字符串。字符串越长精度越高,对应的矩形范围越小。
其实现的思路是这样的,要想把由二维元素表述的位置转变成一维的,并且,相同坐标的点对应的字符串前缀是一样的,那么我去寻找相同位置的时候,可以寻找相同前缀的字符串,字符串的位数也就是位置的精度。由于是一维的表述,方便构成 key: value的索引,便于查找和缓存,效率的提高了至少一个数量级。
对一个地理坐标编码时,按照初始区间范围纬度[-90,90]和经度[-180,180],计算目标经度和纬度分别落在左区间还是右区间。落在左区间则取0,右区间则取1。然后,对上一步得到的区间继续按照此方法对半查找,得到下一位二进制编码。当编码长度达到业务的进度需求后,根据“偶数位放经度,奇数位放纬度”的规则,将得到的二进制编码穿插组合,得到一个新的二进制串。最后,根据base32的对照表,将二进制串翻译成字符串,即得到地理坐标对应的目标GeoHash字符串。
总的来说,geohash是经纬度的一维形式,代表一个坐标。
根据经纬度计算GeoHash二进制编码
地球纬度区间是[-90,90], 科兴的纬度是22.542644,可以通过下面算法对纬度39.928167进行逼近编码:
1)区间[-90,90]进行二分为[-90,0),[0,90],称为左右区间,可以确定39.928167属于右区间[0,90],给标记为1;
2)接着将区间[0,90]进行二分为 [0,45),[45,90],可以确定39.928167属于左区间 [0,45),给标记为0;
3)递归上述过程39.928167总是属于某个区间[a,b]。随着每次迭代区间[a,b]总在缩小,并越来越逼近39.928167;
4)如果给定的纬度x(22.542644)属于左区间,则记录0,如果属于右区间则记录1,这样随着算法的进行会产生一个序列1011100,序列的长度跟给定的区间划分次数有关。
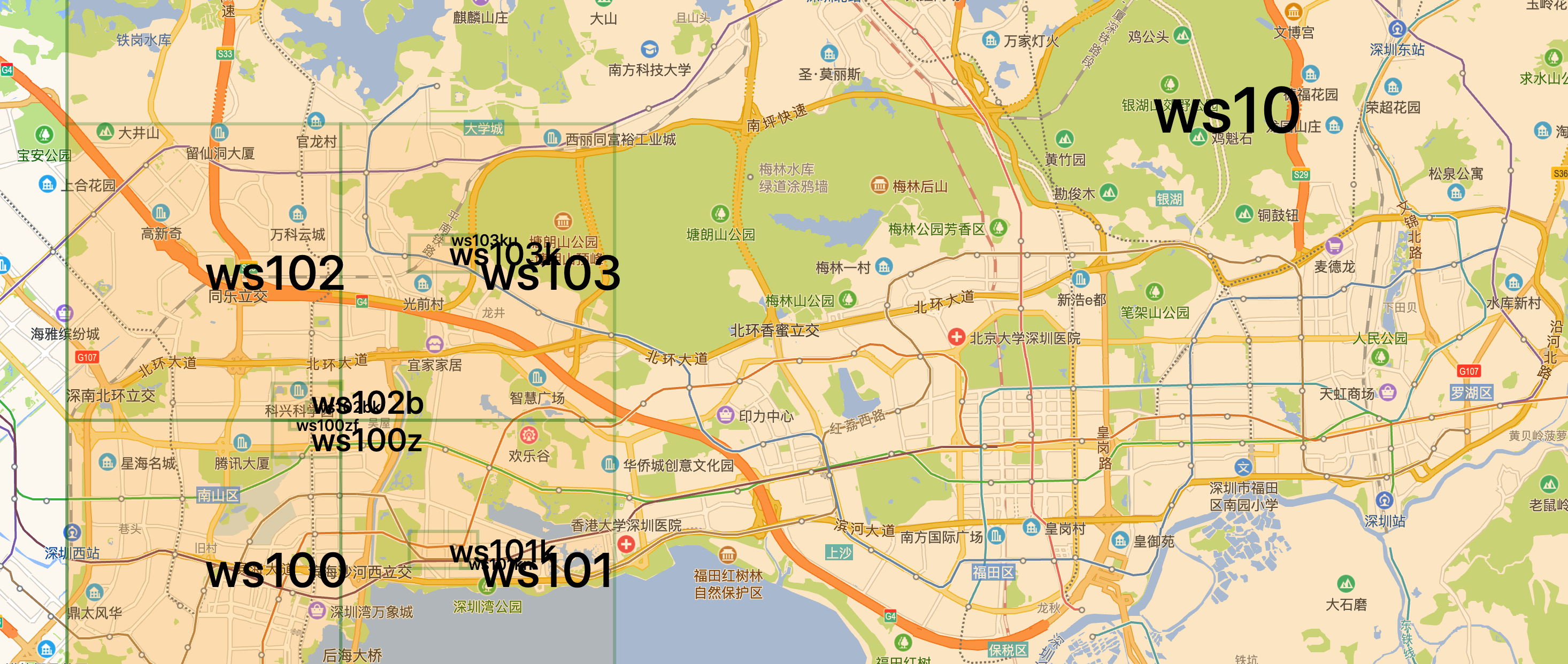
我们按照上面的方法,将位置的GPS转化为一组二进制,经纬度各是一组1010101的串,偶数位放经度,奇数位放纬度,把2串编码组合生成新串。将字符串进行 base32编码就可以得到 ws103这样的 位置代码。
GeoHash Base32编码长度与精度
当geohash base32编码长度为8时,精度在19米左右,而当编码长度为9时,精度在2米左右,编码长度需要根据数据情况进行选择。
可以在类似如下可视化平台查看某个地区的 GeoHash
genhash编码的解析贴一个维基百科的例子:
降维与Z阶曲线
从经纬度到geohash值,我们经历了一个降维的过程,我们知道了如何从一个经纬度去计算一个geohash,那么,为什么可以这么计算呢?
计算机上有一个分形的分支,数学上也有,同时,数学中有一类被称为降维函数的存在,将多维数据映射到一维,同时保留数据点的局部性。
参考: Z阶曲线
比如经纬度降维的过程可以如下证明: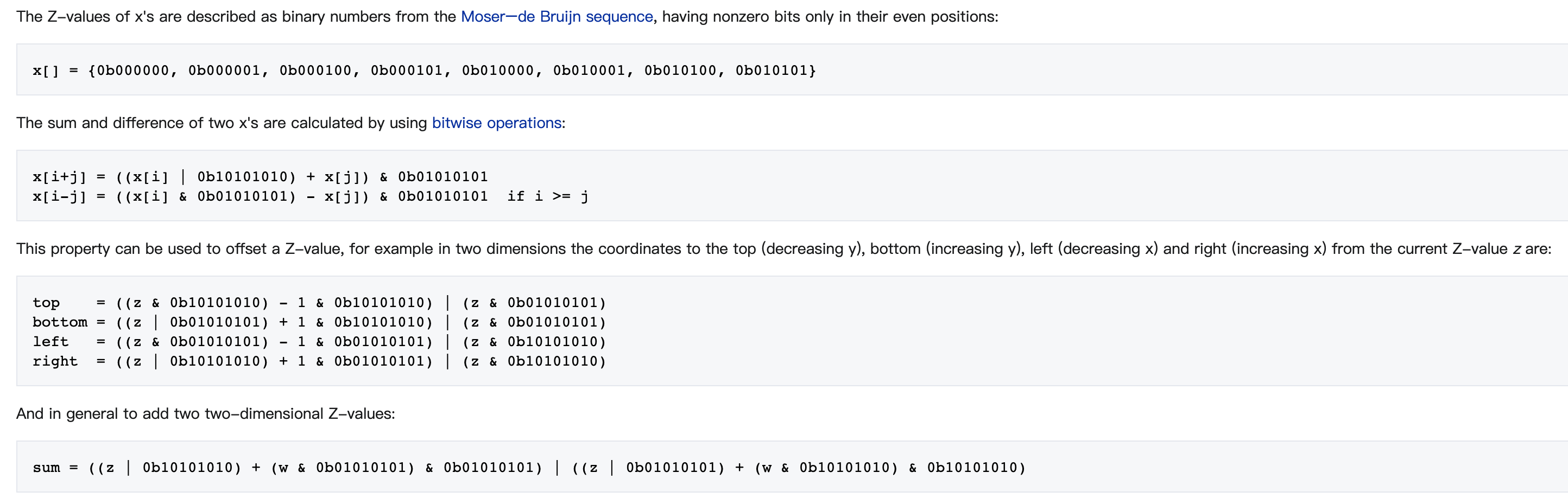
数学基础收到冲击 : )
###
论点:现在的很多玩法很多都是基于几十年前别人的研究项目,想起来之前看到的一句话,你能看到多远的过去,就能看到多远的将来.
