可变基数树技术分享

可变基数树分享

使用可变基数树优化交易订单簿以及使用SIMD硬件加速查找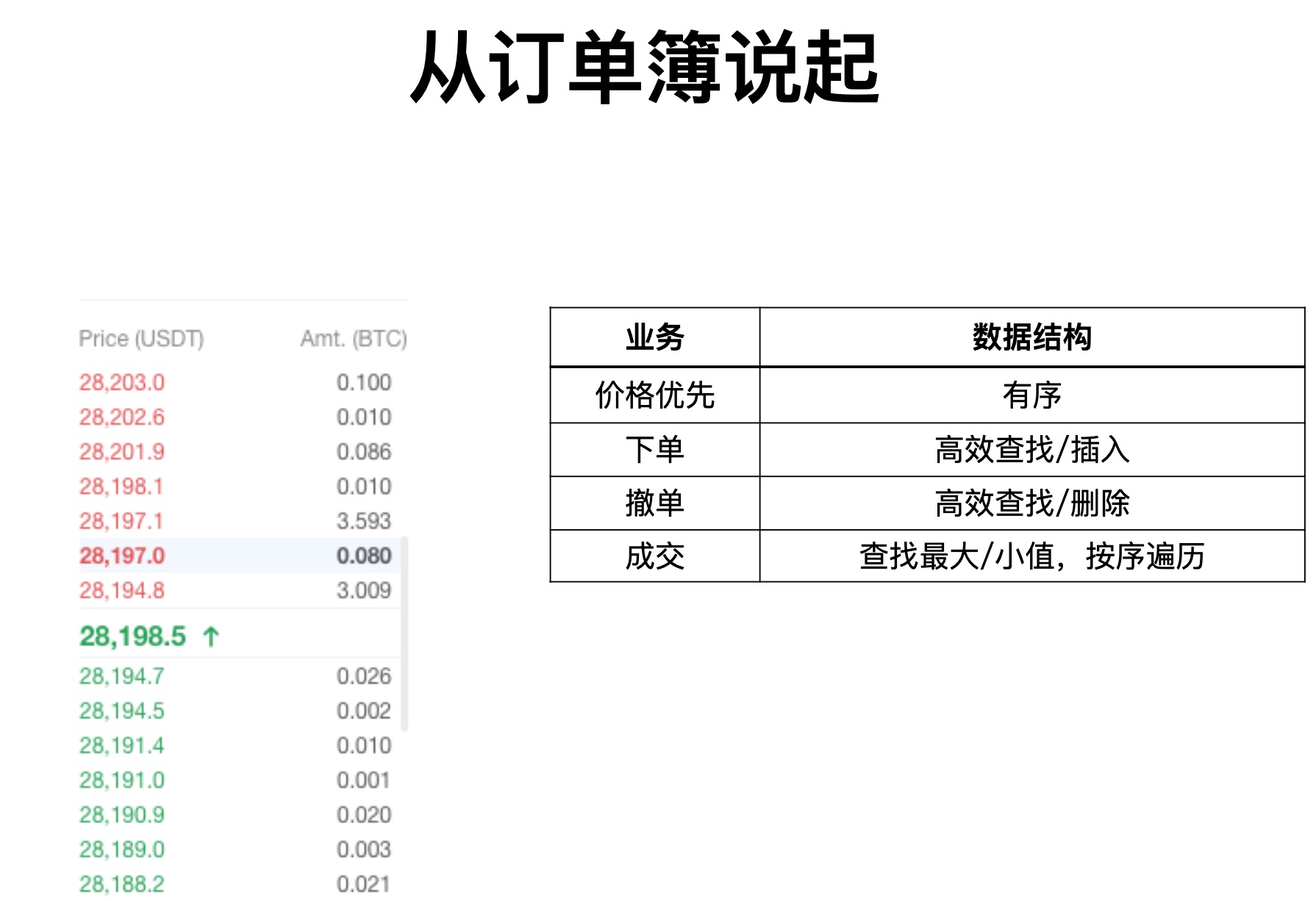

主要参考论文: https://db.in.tum.de/~leis/papers/ART.pdf

背景

内存变得容量更大更便宜，整个数据库/存储引擎可以放到内存
传统的内存数据索引一般是平衡二叉树在现代的硬件上效率不高
另一类索引结构，hash表只支持单点查找，范围查找不好
索引效率是决定性能的关键因素
前言
T树和二叉树硬件支持不好 on modern hardware architectures
B+ tree 缓存敏感，但是update代价比较大
The k-ary search tree and the Fast Architecture Sensitive Tree (FAST) 使用数据级并行性与单指令多数据 (SIMD) 指令同时执行多重比较。此外，FAST 使用的数据布局通过优化利用缓存行和 TLB 来避免缓存未命中。但两种数据结构都不能支持增量更新。
哈希表随机分散了键，只支持点查询；另一个问题是大多数哈希表不能优雅地处理增长
GPU 可以实现比 CPU 更高的吞吐量。然而，使用 GPU 作为专用索引硬件还不实用，因为 GPU 的内存容量有限，与主存的通信成本很高，
Trie

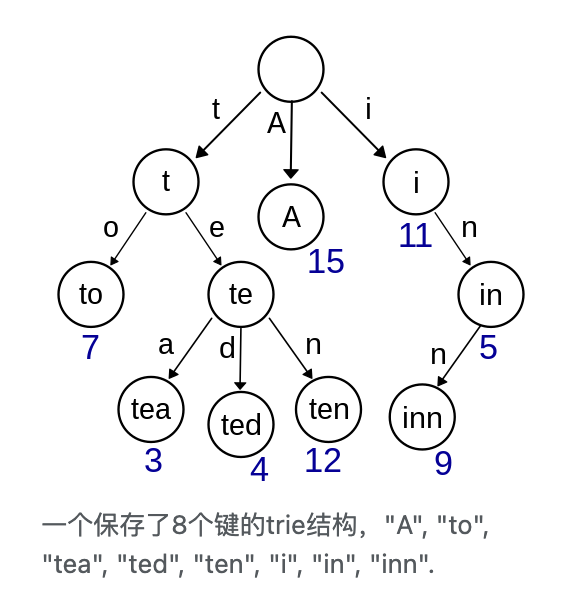
Trie 大多数研究都集中在索引字符串上，但我们的目标是索引其他数据类型。因此，我们更喜欢术语基数树而不是 trie，因为它强调了与基数排序算法的相似性，并强调可以索引任意数据而不仅仅是字符串。
在实际实现上，“基” 一般是 2^K中的 K，下面解释。

基数数是什么结构？

按字母顺序排列的字典书中的拇指索引。一个词的第一个字符可以直接用来跳到所有以该字符开始的词。在计算机中，这个过程可以用接下来的字符重复进行，直到找到一个匹配的字符。作为这个过程的结果，所有的操作都有O(k)的复杂性，其中k是key的长度。

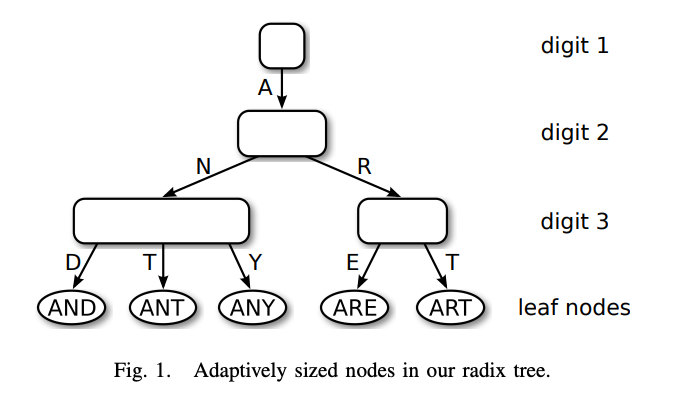
特点：

路径压缩和懒惰扩展，使ART能够通过折叠节点有效地索引长键，从而降低树的高度
根据子节点的数量动态地选择结构
树的高度与Node个数无关，与key长度有关
all insertion orders result in the same tree
key是隐藏的，可以从路径获得
不需要平衡
Key按字典顺序存储
可伸缩的node

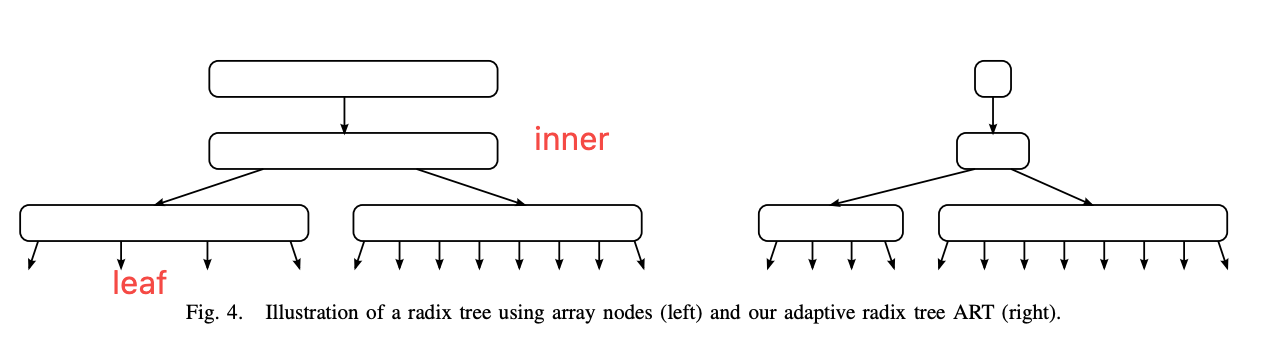
node span

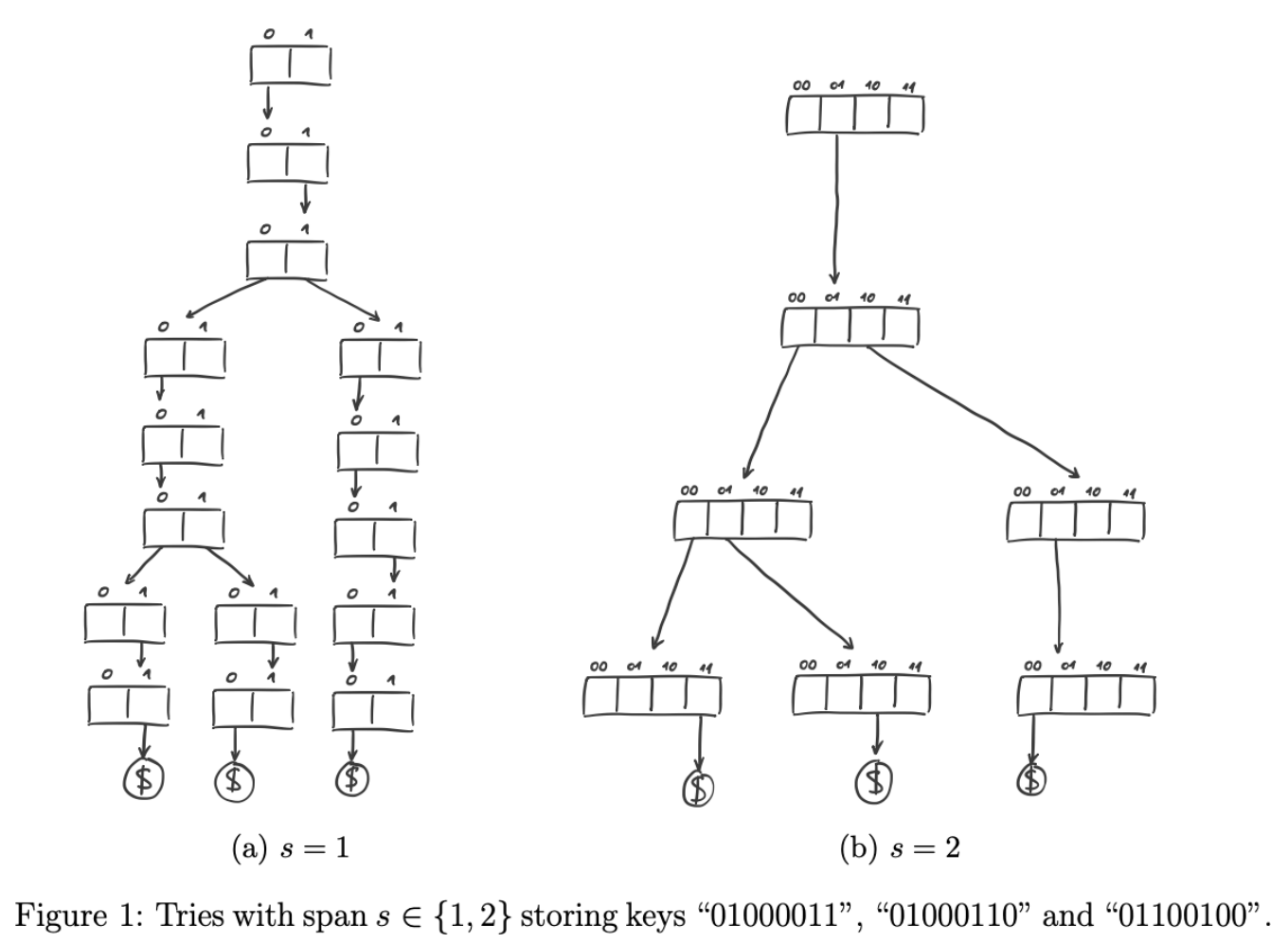
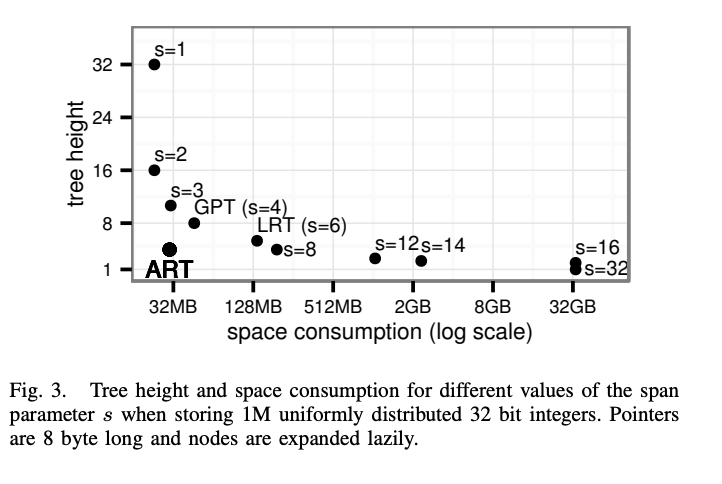
影响因素：

Span越⼤，⾼度越低
Span越⼤，空间占⽤越⼤

问题: 选多大的span？ 1. 折中 2. 可变的node类型
-> 可变基数树 node类型可变
处于性能考虑，节点的类型比较少，如果是几十类，resize的代价会很高

Inner Nodes

插入时，当前node大小没有空间，扩展到大一级的node,同样，缩小时resize到小一级的node。
each inner node has at least two children.
Leaf Nodes

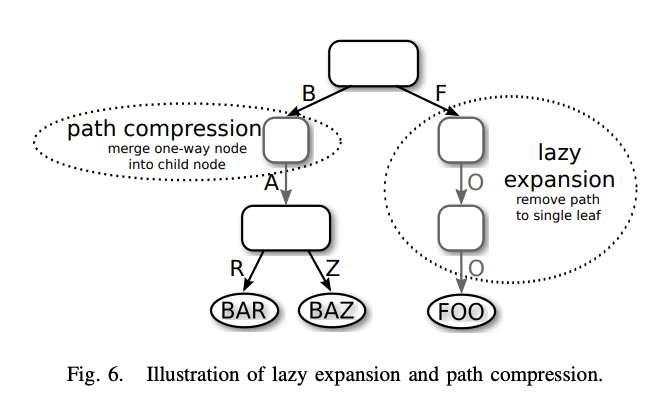
简单的例子

put(0x3FAA01L,"0x3FAA01L");
put(0x3FAA02L,"0x3FAA02L");
put(0x4FAA03L,"0x4FAA03L");

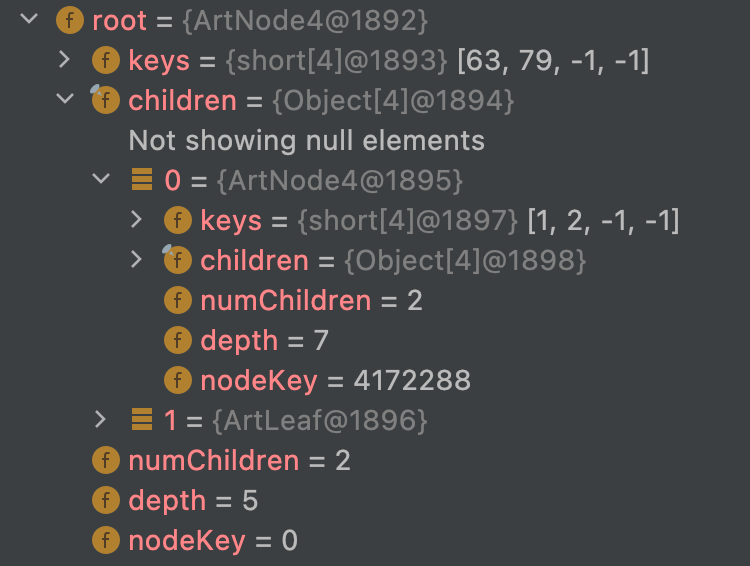
例子二

map.put(2,"2");
map.put(533, "533");
map.put(573, "573");
map.put(40001, "40001");
map.put(40021, "40021");
map.put(40023, "40023");
map.put(40044, "40044");
map.put(40086, "40086");

for(int i = 0;i<20;i++){
    long x = 0x3FCC01 + i;
    map.put(x , String.valueOf(x));
}

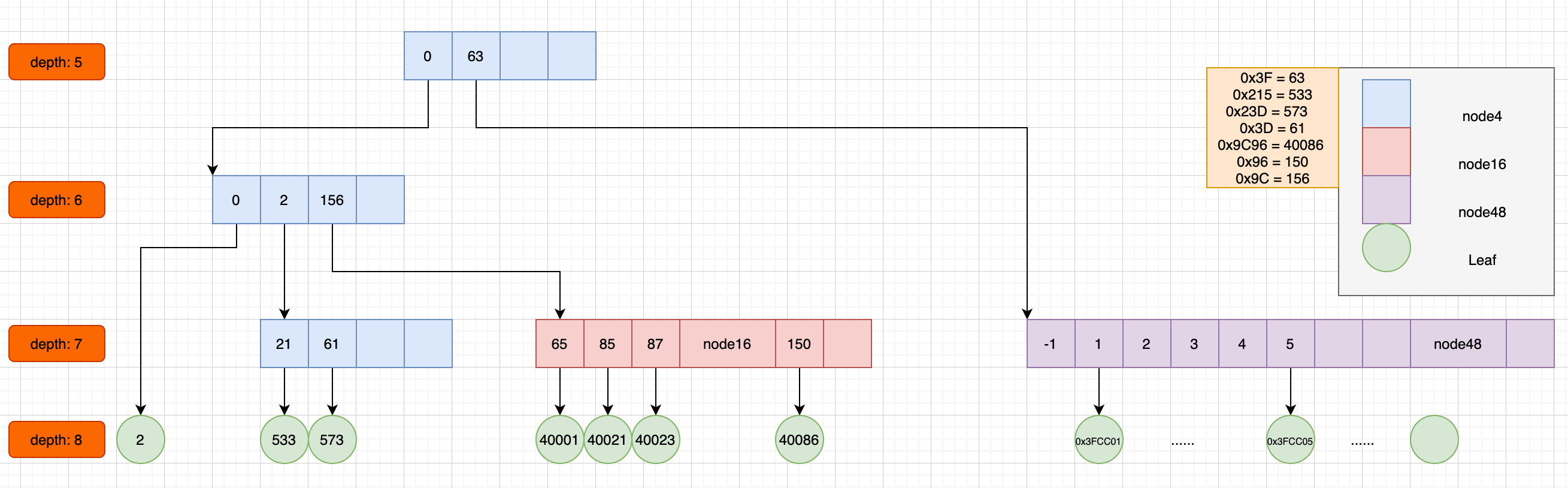
算法

search

get(key)
	cur = root
	while(cur){
		checkPrefix(key) != depth
			return null
		isLeaf(cur)
			return vale
		// 向下递归
		cur = cur.find(key)

	}

Insert

put(key , value){
	leaf = createLeaf(key,value)
	root == null ? root= leaf return
	cur = root
	while(true){
		if (checkPrefix(key) == true ){
			// 替换旧节点
			isLeaf() replace(leaf)

			//cur is inner
			child = cur.findChild(key)
			// 没有子树 branch 
			child == null {
				cur.needGrow() ? grow() 
				cur.put(leaf)
			} else {
            	// 递归向下
				cur = child
        	}
		} else {
			//分裂
			newNode = createNode4
			newNode.put(cur)
			newNode.put(leaf)
			curParent.adjust
		}

	}
}

grow & shrink

grow(){
	node4 -> node16 {
		copy
	}

	node16 -> node48{
		// 规则转换
		key rules transform
		children index build 
	}

	node48 -> node256{
		// 没有keys数组了 children数组index转换
		children index by node48 key
	}
}

分裂

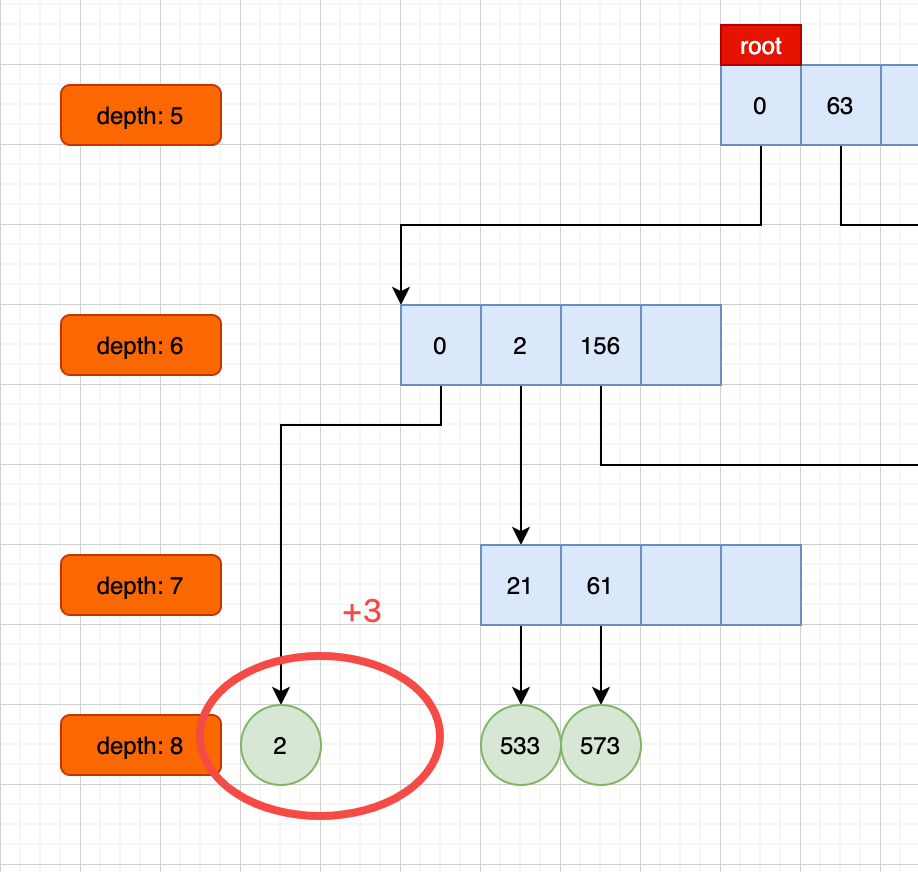
int checkPrefix(long key) {
        //从左到右 多少位是相同的
        //8位一个深度 depth 默认8 ，最深深度
        return Math.min(Long.numberOfLeadingZeros(key ^ nodeKey) / 8, depth);
}
// depth=6带一个Leaf, 再添加一个Leaf，创建一个node4 挂到 parent节点  如上例

性能数据对比

random	ART(ms)	TreeMap(ms)	diff
put (16M keys)	12857	40562	215%
search (16M keys)	7253	25413	250%
foreach (16M keys)	695	2334	235%

put (64k keys)	73	105	43%
search (64k keys)	25	28	12%
foreach (64k keys)	7	14	100%

put (1M keys)	896	1420	58%
search (1M keys)	373	684	83%
foreach (1M keys)	52	73	40%

连续	ART(ms)	TreeMap(ms)	diff
put (16M keys)	1999	4302	115%
foreach (16M keys)	152	192	26%
put (650K keys)	174	191	9%
foreach (650K keys)	17	35	100%

分析性能产生的原因

key越多，差距越大
随机的比连续的差距大

随机的比连续的差距大 –> 考虑缓存的影响。
对比二者的结构：

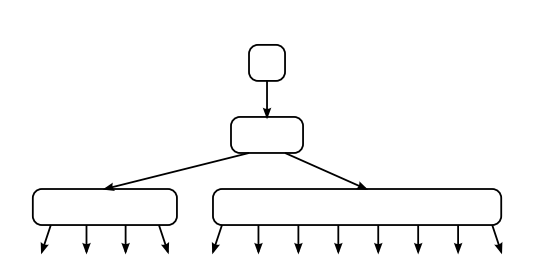
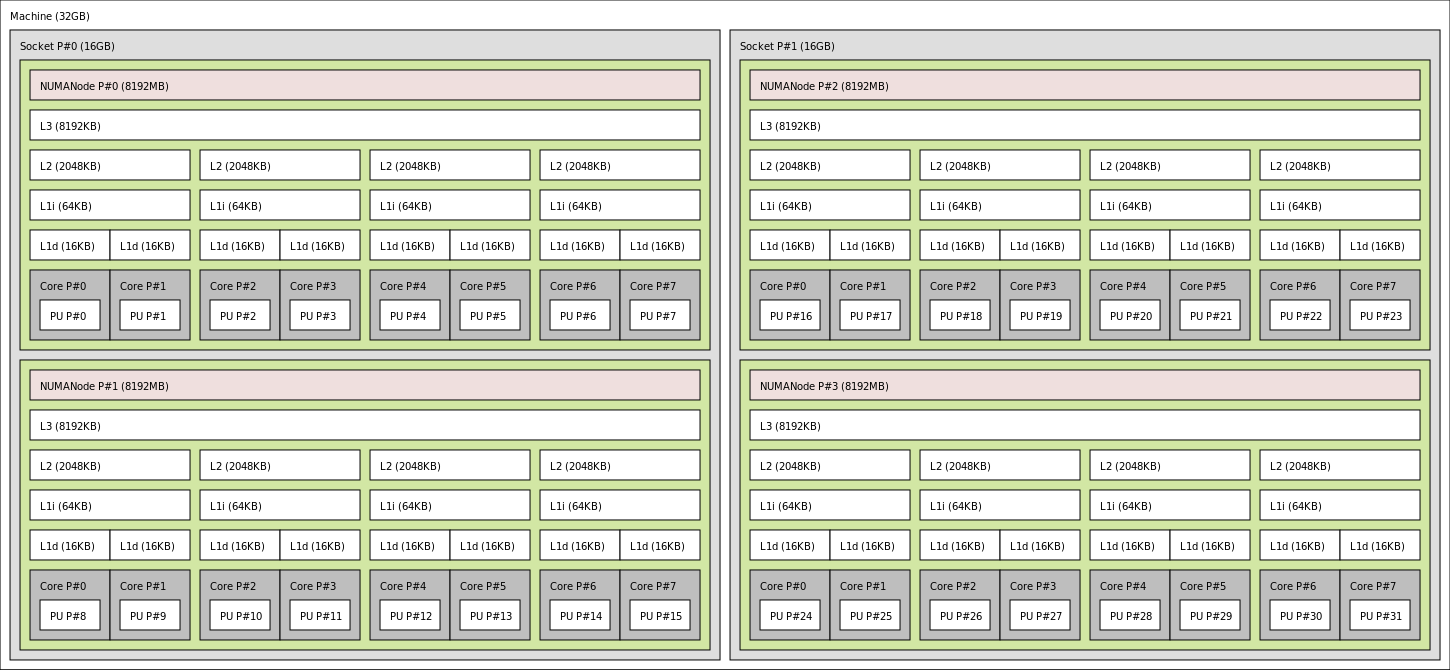
高速缓存存储器结构

撮合服务器 CPU型号是 Intel(R) Xeon(R) Platinum 8369B CPU @ 2.70GHz, intel官网没有（ L3 cache是49M，见附录），应该是订制的，找同类型的CPU参数:

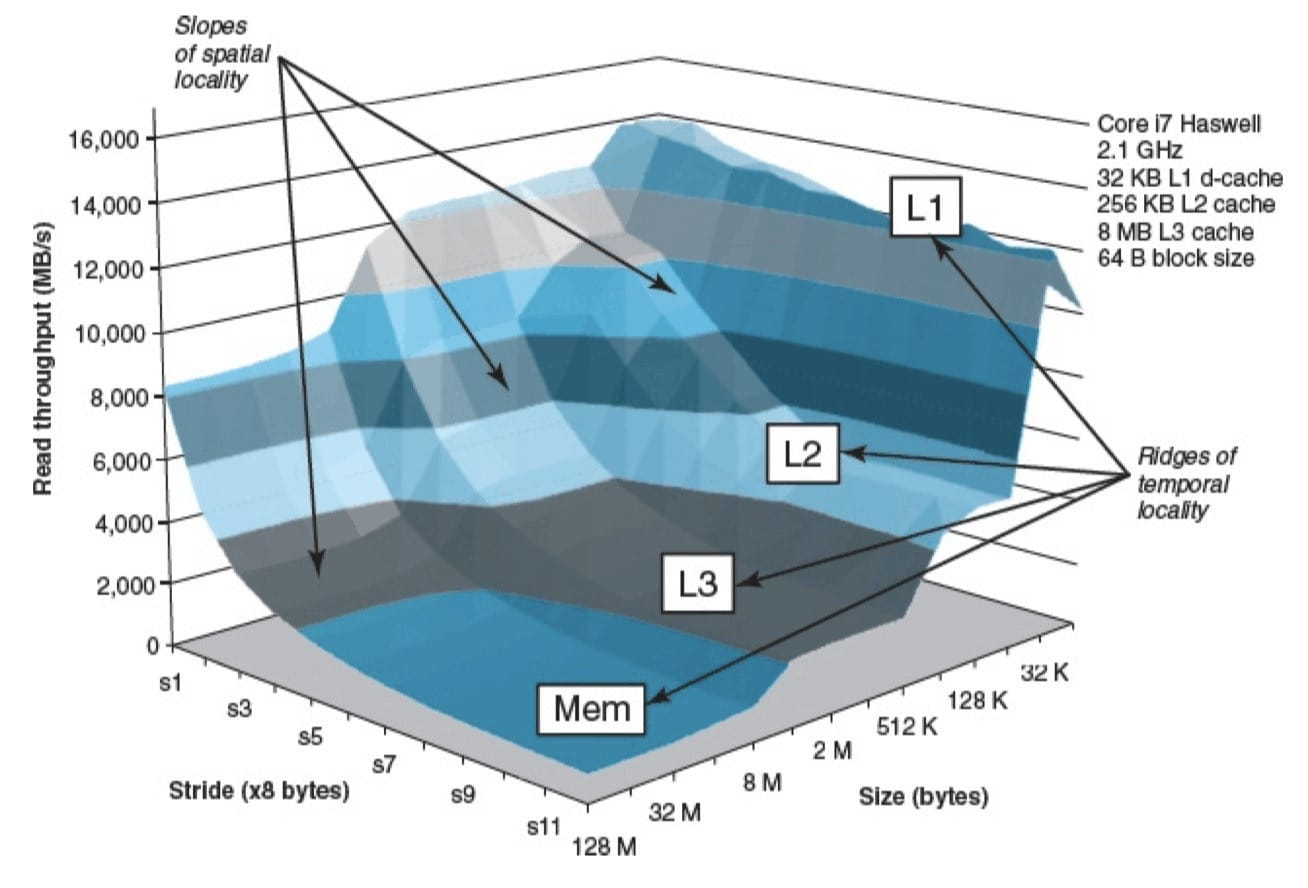
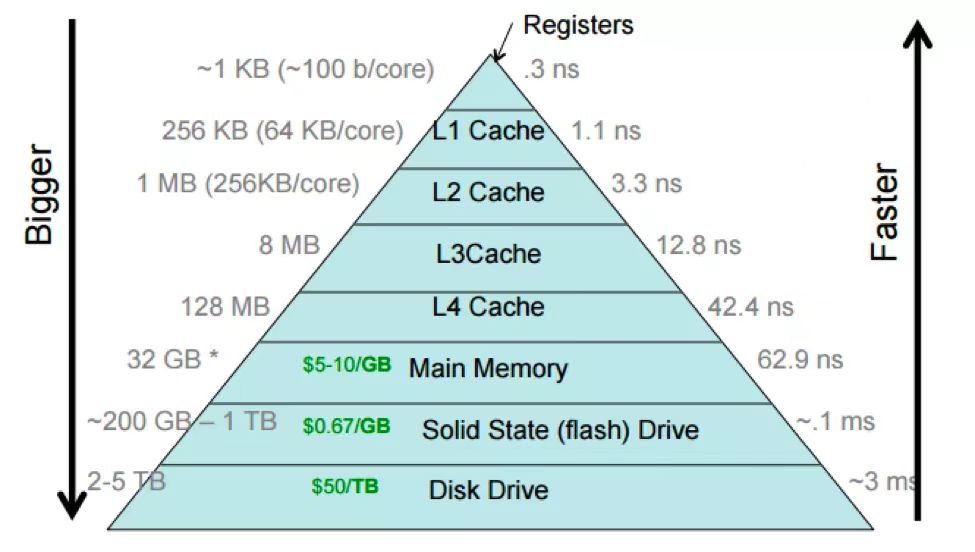
考虑一个计算机系统，其中每个存储器地址有 m 位，形成 M= 2^m个不同的地址。这样一个机器的高速缓存被组织成一个有 S=2^s个高速缓存组（cache set）的数组。每个组包含 E 个高速缓存行（cache line）。每个行是由一个 B=2^b 字节的数据块（block）组成的，一个有效位（valid bit）指明这个行是否包含有意义的信息（为了方便），还有 t = m-(b+s) 个标记位（tag bit）（是当前块的内存地址的位的一个子集)，它们唯一地标识存储在这个高速缓存行中的块。

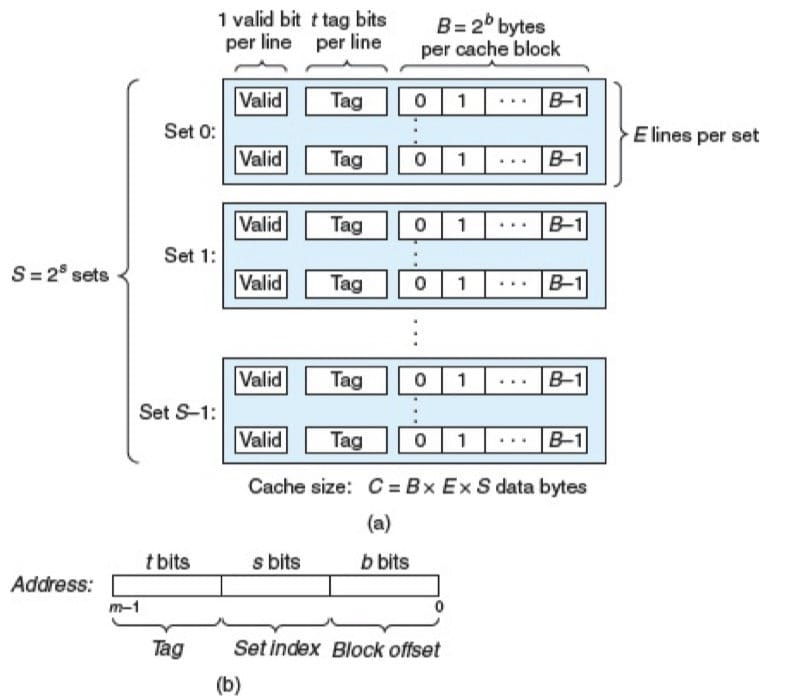
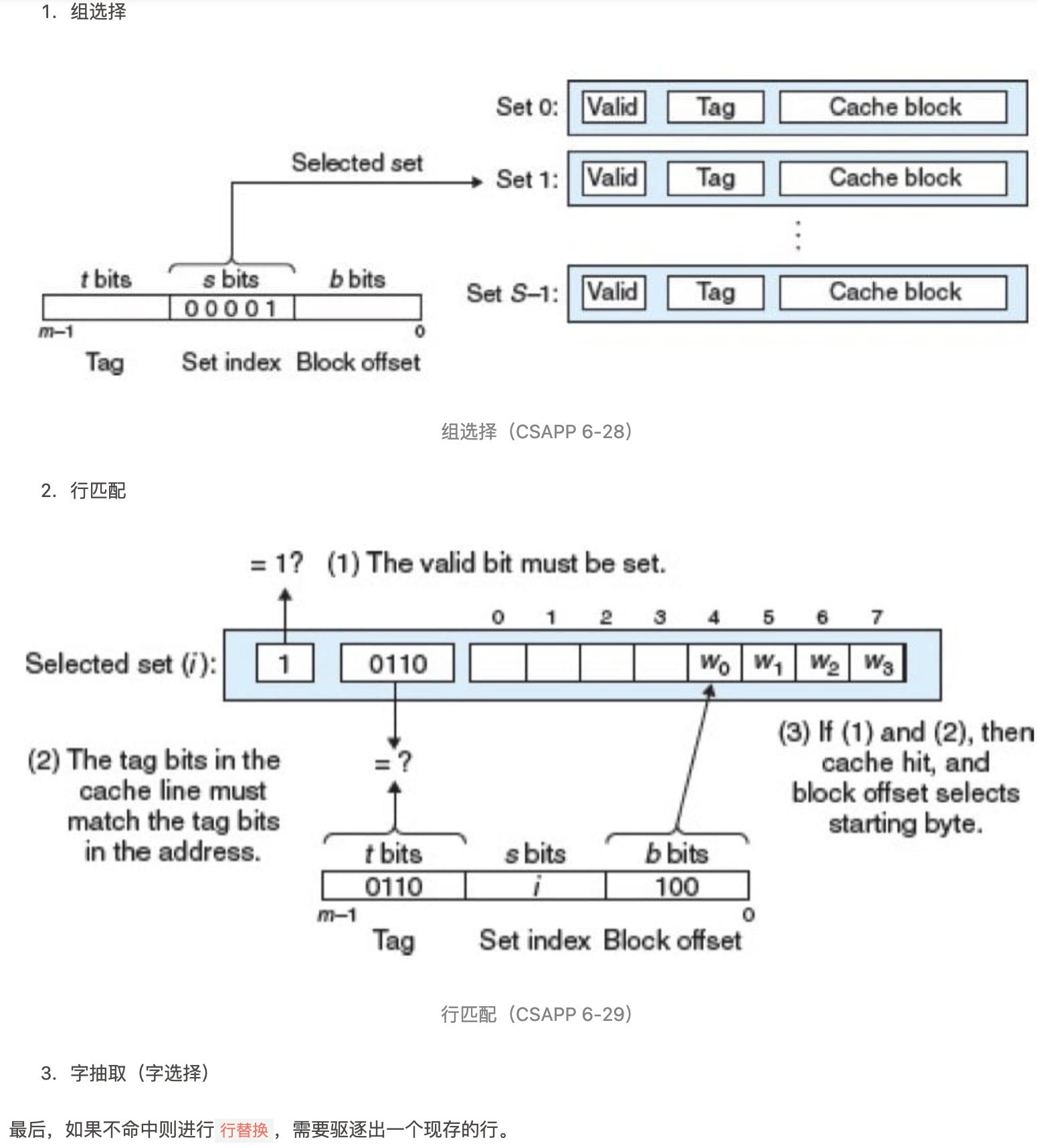
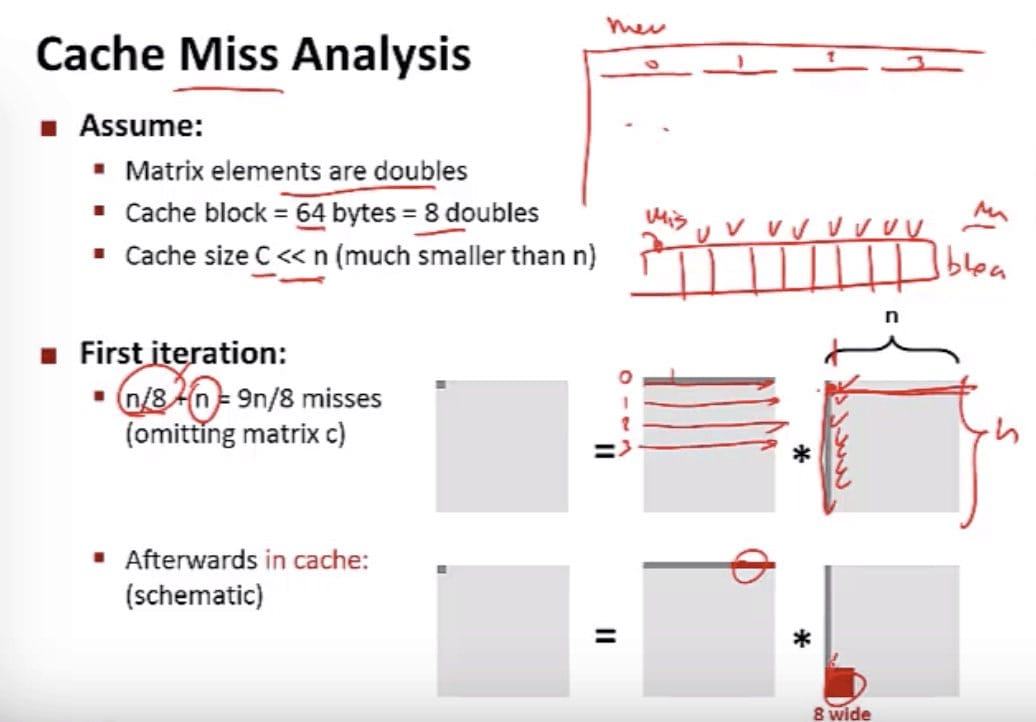
不命中时的行替换

替换组中的哪一行（没有空行）？替换策略：

最不常使用（Least-Frequently-Used，LFU）
最近最少使用（Least-Recently-Used，LRU）

所有这些策略都需要额外的时间和硬件。

另外的优化途径-SIMD

硬件支持

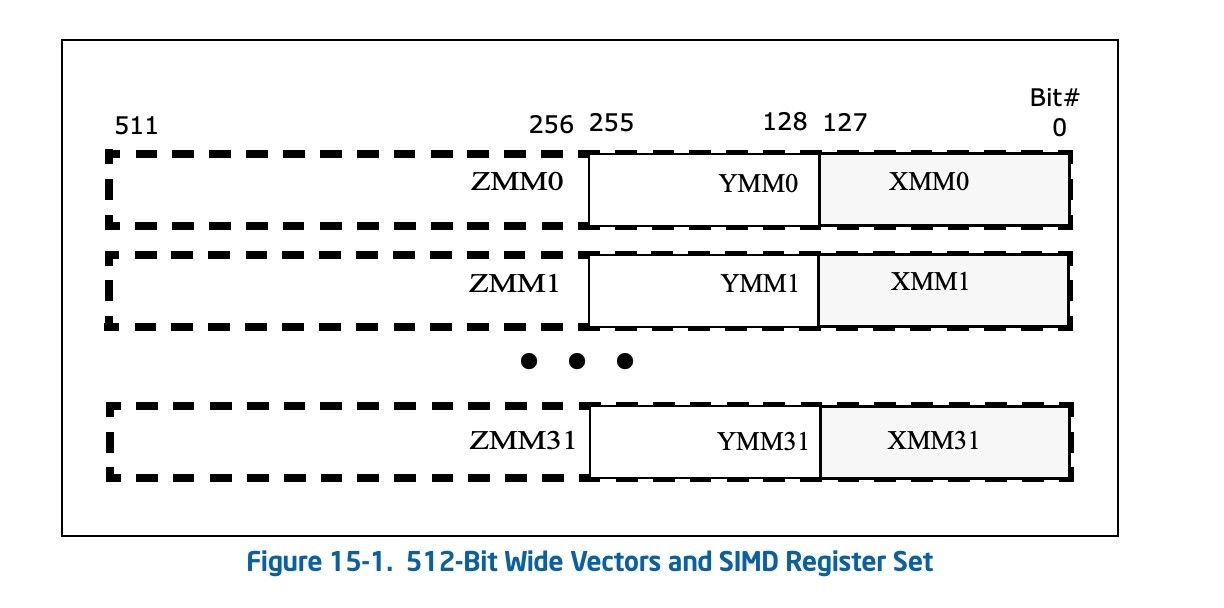
语言支持

Java JEP 417: Vector API (Third Incubator) on jdk17/18

https://openjdk.org/jeps/414

https://openjdk.org/jeps/417

例子

static final VectorSpecies<Integer> SPECIES = IntVector.SPECIES_256;

void multiply(int[] array, int by) {
    int i = 0;
    int bound = SPECIES.loopBound(array.length);
    IntVector byVector = IntVector.broadcast(SPECIES, by);
    for (; i < bound; i += SPECIES.length()) {
        IntVector vec = IntVector.fromArray(SPECIES, array, i);
        IntVector multiplied = vec.mul(byVector);
        multiplied.intoArray(array, i);
    }
    for (; i < array.length; i++) {
        array[i] *= by;
    }
}

Vector Api

组件	items
VectorSpecies	SPECIES_512, 256, 128…
Vector	ShortVector, LongVector
VectorMask	firstTrue() , trueCount() , anyTrue()…
VectorOperators	EQ , LT, GT…

用SIMD 优化 radix tree的查询

   short[] sss = new short[16];
   for(short i = 0; i<16; i++){
       sss[i] = (short) (i*10 + 1);
   }
   // 1 11 21 31 41 51 61 ...
   VectorSpecies<Short> species = ShortVector.SPECIES_256;
   Vector<Short> vecArrays = species.fromArray(sss,0);

// compare 16 keys with one instruction in parallel. 
   int idx = vecArrays.compare(VectorOperators.EQ,51).firstTrue();

node 48、256 search

由于VectorApi不支持指针和bool，对于children多的node，维护一个与children对应的bool flags[childrens]，通过 SIMD批量获取 index后，children.get(index)。

总结

适合Key⻓度固定或较短的场景
较大的Span和垂直压缩显著提高性能
可变的Node大小，显著提高空间利用率，并充分利用SIMD指令
使用数组存储数据对缓存更加友好
只支持字典序，不适合BigDecimal
可变Node与node256 性能近似，与TreeMap比显著提升